Ads
算数の平面図形の勉強をしている時、気になったことがあったのでメモ。
まず、次のような問題がある。
-+-+-+-+-+-+
【問題】
次の四角形で、一本の対角線をひいいたとき、2つの二等辺三角形ができるものはどれか
[正方形、長方形、ひし形、平行四辺形、台形、ふつうの四角形]
-+-+-+-+-+-+
正解は、正方形とひし形である。
で、子供も正解はしたのだが、ちょっと怪訝な顔をしている。
「なんか気になることがあんの?」
「ひし形なんだけどさ、全ての辺の長さが同じだから、対角線を引くと二つの辺は同じ長さになるよね。」
「うん、だから二等辺三角形が2つできるって考えたんだろ?」
「そうなんだけどさあ…、同じ長さ辺以外のもうひとつの辺なんだけど、これが他の2つの辺と同じながさじゃないってことはどうやって説明すればいいのかなあ…」
「へ?それ、説明必要?」
「だってさあ、3つとも同じ長さになっちゃったら、正三角形になるじゃん。」
「ん?そうだけど、正三角形も二等辺三角形の仲間じゃん。」
「え!えーーーー!違うでしょ!」
「ん?そう思う?」
「だって違うものじゃん!」
「そうか…」
なるほど、正三角形は二等辺三角形とは別物だと思っているようだ。
つまり、子供の中では、
・二等辺三角形とは、2つの辺の長さが同じで、もう一つの辺の長さは異なるもの。
・二等辺三角形とは、2つの辺の長さが同じで、正三角形ではないもの。
という定義になっているらしい。
なるほどね。
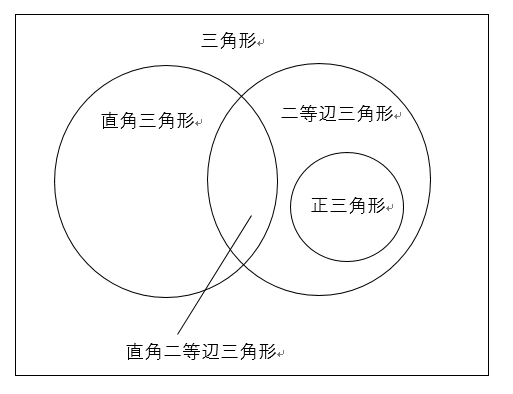
正三角形は二等辺三角形の特殊なもの、ということを説明するのはそう簡単ではない。
「二等辺三角形というのは、2辺の長さが同じもの、という条件があるだけで、他に条件はないんだよ。2辺の長ささえ同じなら、二等辺三角形って呼べるわけ。」
「そうなの?」
「えー、じゃあさ、正三角形ってのは二等辺三角形でもあるわけ?」
「そうだよ。」
「ふうん。そんな風に考えたことなかったよ。」
「そうかあ。正三角形っていいうのは、二等辺三角形の持っている性質を全部持ってるよ。2辺の長さは同じ。底角の角度も同じ。」
「そうか。なんかぴんとこないけど正三角形が二等辺三角形の仲間だってことはわかった。」
「ぴんとこないかあ…。じゃあさ、直角二等辺三角形って二等辺三角形の仲間だと思う。」
「うん、思う。」
「そうだよね。二等辺三角形のうち、頂角、同じ長さの辺が接している頂点の角ね、これが直角だっていう条件が加わったものが直角二等辺三角形だ。」
「そうだよ。」
「これと同じように、二等辺三角形のうち、3つ目の辺も他の2つの辺と同じ長さだっていう条件が加わったのが正三角形だ。」
「うん。なるほど、ちょっとわかった。」
「ちょっと図に書いてみようか。」
ということで、図にしてみた。
で、調子に乗って、四角形も分類してみようということに。
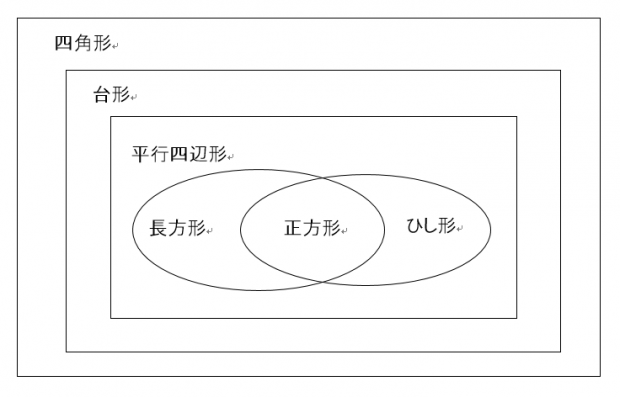
すると、正方形と長方形の関係のところではたと立ち止る。
正方形は長方形の一種なのか?
これについては、
・長方形とは4つの内角が全て直角である四角形
であり、
・正方形は長方形のうちすべての辺の長さが同じもの
という関係だ。
しかし、子供の感覚としては、正方形は長方形の仲間ではない。
これは、正三角形が二等辺三角形の仲間ではないという感覚よりも強いようだ。
確かに、私自身も、長方形には正方形を含まない、という感覚がなくはない。
それは、語感から来るものもある。長方形の「長」という言葉が、何となく「長い四角形」という意味があるからだろうか。
また、推測にしか過ぎないが、小学校低学年?の段階で、正方形という特別な形を理解させるために、長方形との違いを強調するような教育が行われているせいかも知れない。
正方形は長方形の特殊な形である、ということに承服しがたい「感覚」があるようだ。
しかし一方で、正方形はひし形の特殊な形である、ということは、子供も自分も共にすんなり納得できる。
やはり、正方形と長方形の関係には何か強い刷り込みが生じている模様だ。
ともあれ、整理のためにこちらも図にしてみる。
どうも、この辺の概念関係については教科書上できちんと説明されているものでもないようだ。
どうも敢えてそうしているのかな、と思う節もあるのだが、ちょっと気持ち悪い気はした。

はじめまして。通りすがりの現役小学校教員です。
「四角形や三角形の包摂関係は小学校では教えていない」について、
実は、採用されている教科書会社によって扱いが違います。
メジャーな東京書籍の「4年生」では触れていませんが、
それほどでもない学校図書の「4年生」ではベン図を使ってまとめてあります(コラム的な扱いですが)。
私はやはり、互いの関係を理解することが必要だと思っているので、
教室の壁にベン図を掲示しています。
ご参考までに。
長らくブログを放置してしていました。すみません。
もう読まれていないとは思いますが…コメントありがとうございます。
参考になる情報ありがとうございます。
はじめまして。
詳細はここに書きました。
http://8254.teacup.com/kakezannojunjo/bbs/t44/l50
1970年代は算数で「集合」が教えられていて、四角形の包含関係も明示的の教えられていたようです。私自身も教わった記憶があります。
しかしその後、「正方形が長方形であることを理解するのは、子供には難しいから」ということで、このことが姪なくに教えられなくなりました。
それはいいのですが、「正方形は長方形だとは教えない」というのが、どういうわけか一部で「正方形は長方形ではないと教える」となっているようです。
長方形を、正方形を除外する形で定義することは可能ですが、算数の教科書では、長方形の定義を4つの角が直角の四角形としてあるので、これを素直に解釈したら、正方形は長方形となります。
それでいながら、正方形は長方形ではないと教えるというのはおかしな話だと思います。
他にも、正三角形を二等辺三角形の仲間と捉えた答案がバツになったという事例もあります。
「正三角形が二等辺三角形であることは子供には難しい」と言う話が、なぜ「正三角形を二等辺三角形と認識するとバツにする」となるのか全く理解できません。
別件ですが【次の四角形で、一本の対角線をひいいたとき、2つの二等辺三角形ができるものはどれか】も問題文が曖昧ですね。長方形や台形でも条件を満たす場合があるわけで、
【次の四角形で、一本の対角線をひいいたとき、かならず2つの二等辺三角形ができるものはどれか】
の方が曖昧さが軽減すると思います。
はじめまして。
厳密に教えず棚上げするというのも気持ち悪いですが、おっしゃる通り、正方形は長方形でないとか、正三角形は二等辺三角形ではないとかと教えることはもっとおかしな話ですね。これでは、長方形や二等辺三角形の定義の方に新たな条件を加える必要が出てきてしまいます。
正方形が長方形であること、正三角形が二等辺三角形であることを理解することが「小学生にとって難しい」ことなのかどうか自体に疑問を感じます。子供の成長に合わせて段階的に理解させるというしっかりとした考えがあるなら良いですが、教える側の都合で知識の厳密さをないがしろにするのだとすれば問題ではないかと思います。
問題文の件、おっしゃる通り「かならず」を入れるべきですね。やはり曖昧さは回避すべきだと思います。
とても勉強になりました。ありがとうございます。
受験しない小学5年生の父親です。
四角形と台形と平行四辺形と長方形(またはひし形)と正方形の包摂関係は、中学ではじめて教えられ、小学校では教えていないようです。
だったら、子どもは、それらの関係について、何も判断していないかというと、そうではなくて、曖昧ながらある関係で理解しています。子どもは、四角形の仲間として、並列的に、四角形の領域を対等に分け合う特殊な四角形とらえていると思います。
さまざまな四角形の色厚紙があり、これを分類しなさいと言われれば、小学生は、正方形の仲間には正方形だけを入れて、長方形の仲間には、正方形でない長方形だけを分類します。長方形のなかまの内部に、さらに正方形の仲間を作るような、複雑なことは考えつかない。小学生には、なかなか期待できない分類方法です。同じものが、同一でない(が重複している)2つのカテゴリーに同時に帰属することが、考え慣れない事態なのだと思います。
正方形が長方形(またはひし形)の、長方形が平行四辺形の、平行四辺形が台形の、台形が四角形の一部であるというような、かなり多層的な階層構造の理解は、やはり、小学生には負担が大きいところがあります。四角形には、正方形やら長方形やらひし形やらのさまざまな四角形がある、というのであれば、四角形一般とその特殊な四角形たちという2層構造なので、小学生も理解しやすいに、ちがいありません。建物でも、多層的なものは、しっかり作らないと崩壊します。平たい建物のほうが安定しています。まだ抽象的な思考になれていない子どもの心も、長方形を正方形の上に置くのではなく、いわば上から押しつぶして、同等のレベルで並べ、広義の長方形の領域を分け合わせるように働くのではないでしょうか。
うちで飼っているアイリッシュテリアがテリアの仲間で、テリアは犬の仲間で、犬はほ乳類の仲間で、ほ乳類は動物の仲間であるといった、多層的な包摂関係は、小学生も理解できそうです。だとしたら、なぜ、正方形が長方形の仲間であるというのは、理解しにくいのでしょうか。その1つの理由は、正方形以外に、名前が付いた、特殊な長方形の名前がないからではないでしょうか。テリアには、アイリッシュテリアだけでなく、スカイテリアもブルテリアもいます。犬には、土佐犬もブルドッグもビーグルチワワもいます。もう1つは、長方形は縦と横の辺の長さが一般的には一致しないが、たまたま一致している場合があって、それが正方形だ、というところが、わかりづらいことだと思います。
ご指摘のように、長方形の「長」という漢字の意味が、そのような包摂関係の理解を妨げているということも、あると思います。直角二等辺三角形は二等辺三角形の特殊な場合であるというのは、小学生にもすんなり理解できるのではないでしょうか。というのも、「直角二等辺三角形」という語の中には、「二等辺三角形」という語があり、それに「直角」という限定が付いているだけだからです。「とがった三角形」が、三角形の特殊な場合であることが理解しやすいのと同様です。「長方形」という語の代わりに、「方形」という語を用いることにすれば、「(正)方形」はその特殊な場合であることが、より容易に理解されるに違いありません。
エムエムさん、こんにちは。
おっしゃる通り、小学生にとって長方形と正方形は同等のレベルで並列しているカテゴリーというイメージだと思います。厳密ではないにせよ、語感等から、あるいは学校での取り扱い方からも、包摂関係があるという理解はないなあと思います。
「長方形」の代わりに「方形」と呼ぶことにするというのは、とても良い案ですね。実際、「長方形」という語は、図形の概念関係を理解するのには妨げになっている気もします。そのような観点で命名されている訳ではないのでしょうね。
現時点では意識的に子供には厳密に教えないでおきましたが、このような問題は、図形の理解、算数の理解、ということを超えて、論理的な概念関係の理解等にも必要となってくるものだと思いますので、少しずつ色々な例に触れながら考える力がついていけば、と思います。
そういう意味でも、犬の例、とてもわかりやすいですね。
参考にします。ありがとうございます。
とても解り易い解説ですね、子どもさんのつまずきや疑問が晴れるようなナイス解説だと思います。
私の認識が違うのかも知れませんが
最後のベン図で台形でくくってしまうのはマズいんじゃないでしょうか?
ぷっちーさん、こんにちは。子供の疑問に接すると、自分自身がクリアになっていない部分があることにも気づかされますね。意外と悩みました。
四角形のベン図の件ですが、「台形は、一組の対辺が互いに平行である四角形」「平行四辺形は、二組の対辺がそれぞれ互いに平行である四角形」ということで、平行四辺形は台形の特殊なもの、概念的には包摂されるもの、と考えています。
一方で、台形を「一組のみの対辺が平行である四角形」と定義すると、平行四辺形は台形の仲間ではないということになります。世の中には実際そのように定義しているものもあるようです。正方形が長方形に含まれるかの問題と同じですね。微妙です…。
とりあえず、wikipediaなどネットで調べながら(苦笑)上の図のようにしたのですが、学校教育では図形の概念関係を厳密に教えていないようで、そのため私自身も感覚的には?となる部分もなくはありません。学校教育でそうしているのには何か意図があるのかも知れず…そのため、特に四角形のベン図の方は、あえて子供には厳密に教えないようにしておきました。